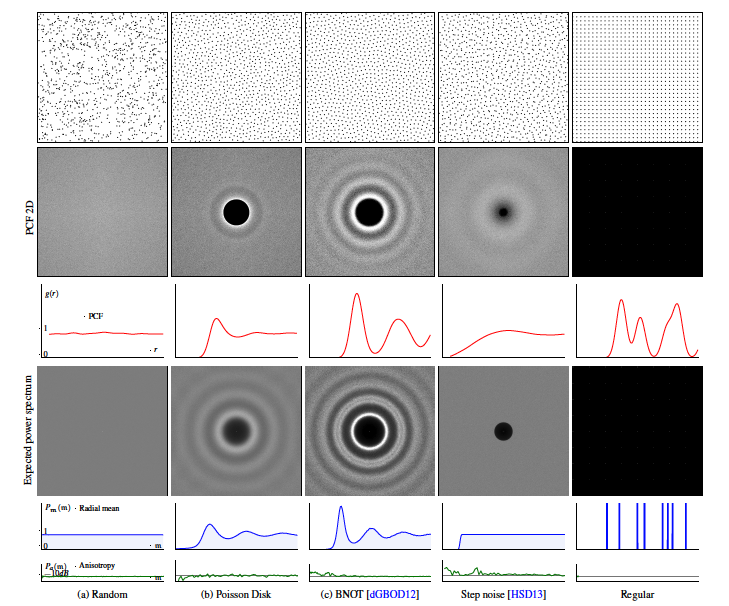
Analysis of Sample Correlations for Monte Carlo Rendering
In this paper, we aim at providing a comprehensive and accessible overview of the techniques developed over the last decades to analyze such correlations, relate them to error in integrators, and understand when and how to use existing sampling algorithms for effective rendering workflows.
May 6, 2019
Eurographics 2019
Authors
Gurprit Singh (Max-Planck Institute for Informatics, Saarbrücken)
Cengiz Öztireli (Disney Research)
Abdalla G.M. Ahmed (KAUST)
David Coeurjolly (Université de Lyon / CNRS)
Kartic Subr (University of Edinburgh)
Oliver Deussen (University of Konstanz)
Victor Ostromoukhov (Université de Lyon / CNRS)
Ravi Ramamoorthi (University of California, San Diego)
Wojciech Jarosz (Dartmouth College)
Analysis of Sample Correlations for Monte Carlo Rendering
Modern physically based rendering techniques critically depend on approximating integrals of high dimensional functions representing radiant light energy. Monte Carlo based integrators are the choice for complex scenes and effects. These integrators work by sampling the integrand at sample point locations. The distribution of these sample points determines convergence rates and noise in the final renderings. The characteristics of such distributions can be uniquely represented in terms of correlations of sampling point locations. Hence, it is essential to study these correlations to understand and adapt sample distributions for low error in integral approximation. In this work, we aim at providing a comprehensive and accessible overview of the techniques developed over the last decades to analyze such correlations, relate them to error in integrators, and understand when and how to use existing sampling algorithms for effective rendering workflows.