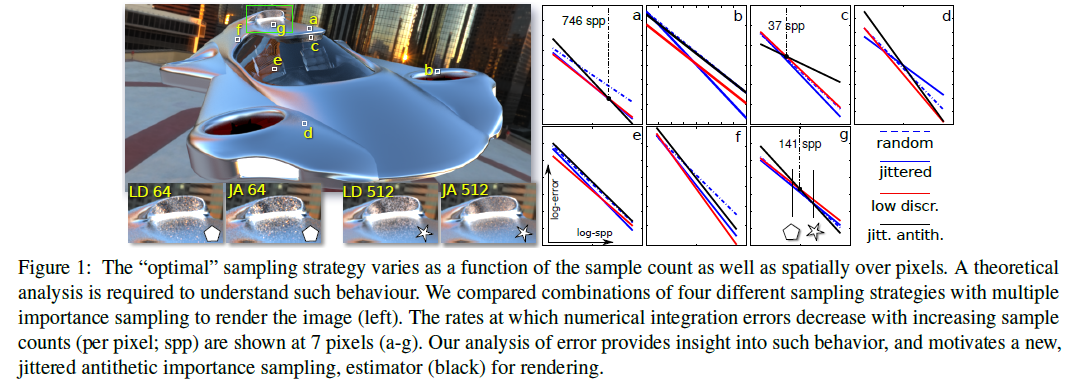
Error analysis of estimators that use combinations of stochastic sampling strategies for direct illumination

We present a theoretical analysis of error of many combinations of Monte Carlo estimators used in image synthesis.

We present a theoretical analysis of error of many combinations of Monte Carlo estimators used in image synthesis. Of these, importance sampling (IS) and multiple importance sampling (MIS) are popular variance-reduction strategies. Unfortunately, neither strategy improves the rate of convergence of Monte Carlo integration. Jittered sampling (a type of stratified sampling), on the other hand, is known to improve the convergence rate. Most rendering software optimistically combines IS with jittered sampling, hoping to achieve both. We derive the exact error of the combination of IS and MIS with jittered sampling. In addition, we analyse and demonstrate a further benefit of introducing negative correlations (antithetic sampling) between estimates to the convergence rate. As with IS, antithetic sampling is known to reduce error for certain classes of integrands without affecting the convergence rate. In this paper, our analysis and experiments reveal that IS and antithetic sampling, if used judiciously and in conjunction with jittered sampling, may improve convergence rates. We show the impact of such combinations of strategies on the convergence rate of estimators for direct illumination.