An Approximate Computing Technique for Reducing the Complexity of a Direct-Solver for Sparse Linear Systems in Real-Time Video Processing
This paper focuses on reducing the computational complexity of a direct Cholesky-decomposition-based solver.
June 1, 2014
Design Automation Conference (DAC) 2014
Authors
Michael Schaffner (Disney Research/ETH Joint PhD)
Frank K. Gürkaynak (ETH Zurich)
Aljoscha Smolic (Disney Research)
Hubert Kaesliny (ETH Zurich)
Luca Beniniy (ETH Zurich)
An Approximate Computing Technique for Reducing the Complexity of a Direct-Solver for Sparse Linear Systems in Real-Time Video Processing
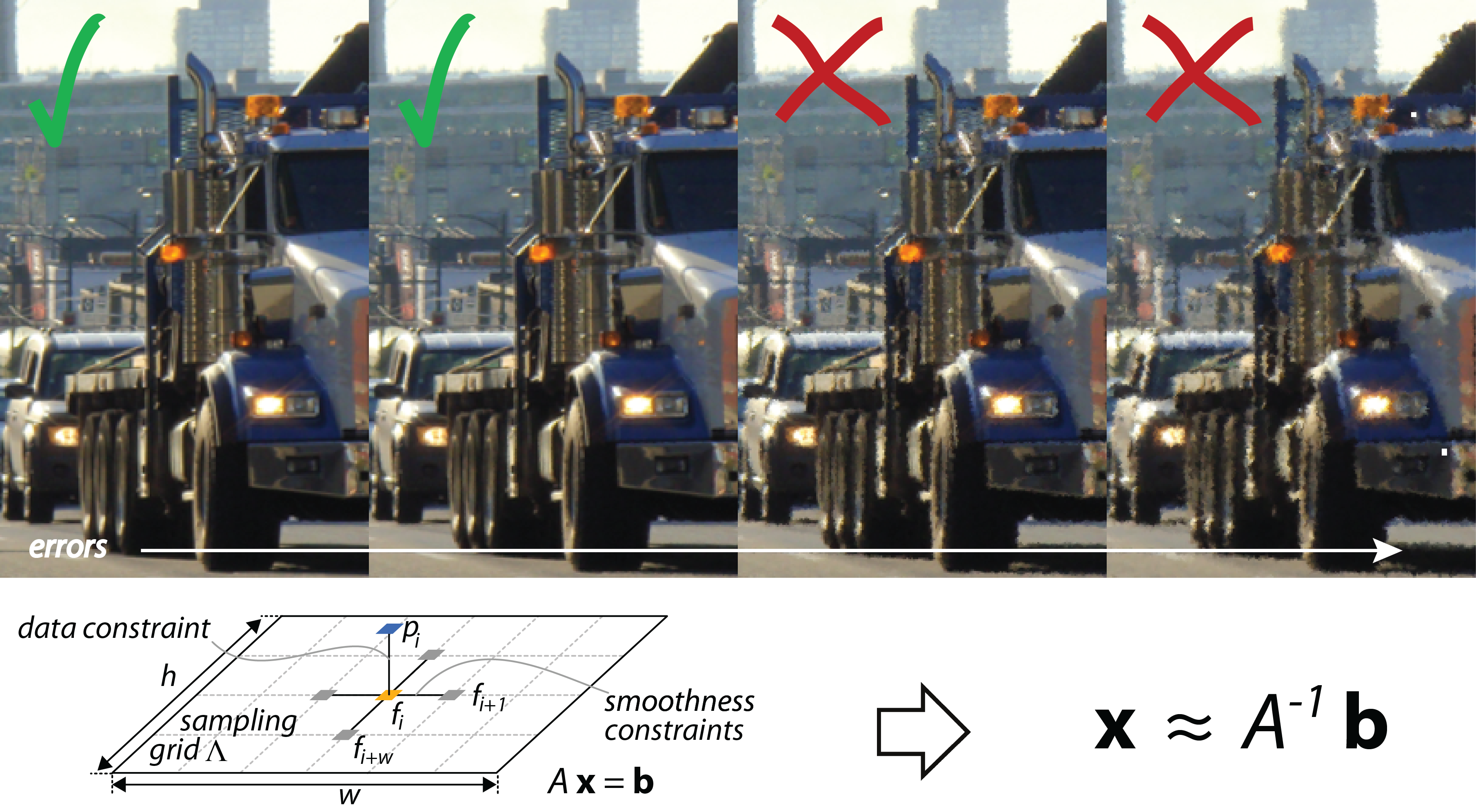
Many video processing algorithms are formulated as least squares problems that result in large, sparse linear systems. Solving such systems in real time is very demanding. This paper focuses on reducing the computational complexity of a direct Cholesky-decomposition-based solver. Our approximation scheme builds on the observation that, in well-conditioned problems, many elements in the decomposition nearly vanish. Such elements may be pruned from the dependency graph with mild accuracy degradation. Using an example from image-domain warping, we show that pruning reduces the amount of operations per solve by over 75 %, resulting in significant savings in computing time, area or energy.